Java Fibonacci examples

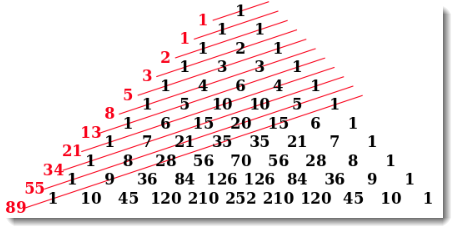
Fibonacci number – Every number after the first two is the sum of the two preceding.

Few Java examples to find the Fibonacci numbers.

1. Java 8 stream

1.1 In Java 8, we can use Stream.iterate to generate Fibonacci numbers like this :

	Stream.iterate(new int[]{0, 1}, t -> new int[]{t[1], t[0] + t[1]})
		.limit(10)
		.forEach(x -> System.out.println("{" + x[0] + "," + x[1] + "}"));

Output

{0,1}
{1,1}
{1,2}
{2,3}
{3,5}
{5,8}
{8,13}
{13,21}
{21,34}
{34,55}

P.S Review the above output, the first value is what we wanted.

1.2 Final version.

	Stream.iterate(new int[]{0, 1}, t -> new int[]{t[1], t[0] + t[1]})
		.limit(10)
		.map(t -> t[0])
		.forEach(x -> System.out.println(x));

Output

0
1
1
2
3
5
8
13
21
34

1.3 Sum all the Fibonacci numbers

	int sum = Stream.iterate(new int[]{0, 1}, t -> new int[]{t[1], t[0] + t[1]})
		.limit(10)
		.map(t -> t[0])
		.mapToInt(Integer::intValue)
		.sum();

    System.out.println("Total : " + sum);

Output

Total : 88

1.4 Join with commas.

String collect = Stream.iterate(new int[]{0, 1}, t -> new int[]{t[1], t[0] + t[1]})
                .limit(10)
                .map(t -> t[0])
                .map(String::valueOf) // convert to string
                .collect(Collectors.joining(", "));

        System.out.println("Result : " + collect);

Output

Result : 0, 1, 1, 2, 3, 5, 8, 13, 21, 34

1.5 A function to create a List of Fibonacci numbers.

package com.mkyong.concurrency;

import java.util.List;
import java.util.stream.Stream;

import static java.util.stream.Collectors.toList;

public class Fibonacci {

    public static List<Integer> getFibonacci(int series) {
        return Stream.iterate(new int[]{0, 1}, t -> new int[]{t[1], t[0] + t[1]})
                .limit(series)
                .map(n -> n[0])
                .collect(toList());
    }

    public static void main(String[] args) {

        List<Integer> fibonacci = getFibonacci(10);
        fibonacci.forEach(x -> System.out.println(x));

    }

}

Output

0
1
1
2
3
5
8
13
21
34

1.6 The type int and long are not enough to store larger Fibonacci numbers. Below is the BigInteger example to find the first million Fibonacci numbers.

package com.mkyong.concurrency;

import java.math.BigInteger;
import java.util.stream.Stream;

public class Fibonacci {

    public static BigInteger getFibonacci(int series) {
        return Stream.iterate(new BigInteger[]{
                BigInteger.ZERO, BigInteger.ONE}, t -> new BigInteger[]{t[1], t[0].add(t[1])})
                .limit(series)
                .map(n -> n[1]) // find, we need n[1]
                .reduce((a, b) -> b).orElse(BigInteger.ZERO);

    }

    public static void main(String[] args) {
        System.out.println(Fibonacci.getFibonacci(1_000_000));
    }

}

Output

1953282128707757731632014947596256332443... // 208,988 digits!!!, too long to display here

2. Recursive Loop

2.1 Java recursive loop example to create a list of Fibonacci numbers. Good to demo only, this recursive loop is slow.

package com.mkyong.concurrency;

public class Fibonacci {

    public static int fib(int n) {
        if (n <= 1) return n;
        else return fib(n - 1) + fib(n - 2);
    }
    
    public static void main(String[] args) {

        for (int i = 0; i < 10; i++) {
            System.out.println(fib(i));
        }

    }


}

Output

0
1
1
2
3
5
8
13
21
34

2.2 How it works?

fib(n) = fib(n - 1) + fib(n - 2);

fib(5) = fib(4) + fib(3);
fib(4) = fib(3) + fib(2);
fib(3) = fib(2) + fib(1);
fib(2) = fib(1) + fib(0);
fib(1) = 1
fib(0) = 1

3. Normal Loop

3.1 Java normal loop to find the Fibonacci numbers, simple and easy.

package com.mkyong.concurrency;

import java.math.BigInteger;

public class Fibonacci {

    public static int fib(int n) {
        if (n <= 1) return n;

        int previous = 0, next = 1, sum;

        for (int i = 2; i <= n; i++) {
            sum = previous;
            previous = next;
            next = sum + previous;
        }

        return next;
    }

    public static BigInteger fib2(int n) {
        if (n <= 1) return BigInteger.valueOf(n);

        BigInteger previous = BigInteger.ZERO, next = BigInteger.ONE, sum;

        for (int i = 2; i <= n; i++) {
            sum = previous;
            previous = next;
            next = sum.add(previous);
        }

        return next;
    }

    public static void main(String[] args) {

        for (int i = 0; i < 10; i++) {
            System.out.println(fib(i));
        }

        System.out.println("---");

        for (int i = 0; i < 10; i++) {
            System.out.println(fib2(i));
        }

        System.out.println("---");

        System.out.println(fib(100)); //overflow
        System.out.println(fib2(100));
    }

}

Output

0
1
1
2
3
5
8
13
21
34
---
0
1
1
2
3
5
8
13
21
34
---
-980107325
354224848179261915075

References

1. Fibonacci number